Data Structures and Algorithms II. University of Almeria
Version curso.2022
Goals
-
Construct solutions to a problem using the greedy algorithmic method.
-
Compare the implemented algorithms both qualitatively and quantitatively.
-
Carry out an analysis of the efficiency of the solutions provided, and a comparison both from a theoretical and practical point of view.
Requirements
To pass this practice, the following must be done:
-
Remember (from EDA I, the adjacency map) the data structures to implement a network (undirected graph) and its use for problem solving .
-
Know how to implement the greedy scheme on graphs to respond to a specific need (in this case, solving a problem related to a road network).
-
Evaluate the implemented greedy algorithms, using real networks and randomly generated networks.
Problem statement
One of the main practical applications of graphs are networks, for example: the road network, the railway network, communication networks, etc. In this case we have a network of roads that connect all the population centers of the country EDAland, and the need of the Ministry of Infrastructure and Transport of that country is to pave them. But given the current economic crisis in which we are immersed, there is not enough budget to be able to pave all possible roads in the country. After a tough negotiation with the ministry and taking into account the reduced budget available, it has been decided that only some roads will be paved to be able to go from one population center to another following a paved route, and also, the smallest possible budget will be dedicated to the realization of the work. Another aspect to consider is that the inhabitants of the country do not mind traveling a long distance, since now they move by bicycle (given the high price of fuel), which is very beneficial for health and the environment. The Minister is very interested in knowing which roads need to be paved to connect all possible population centers in the country with the lowest possible budget.
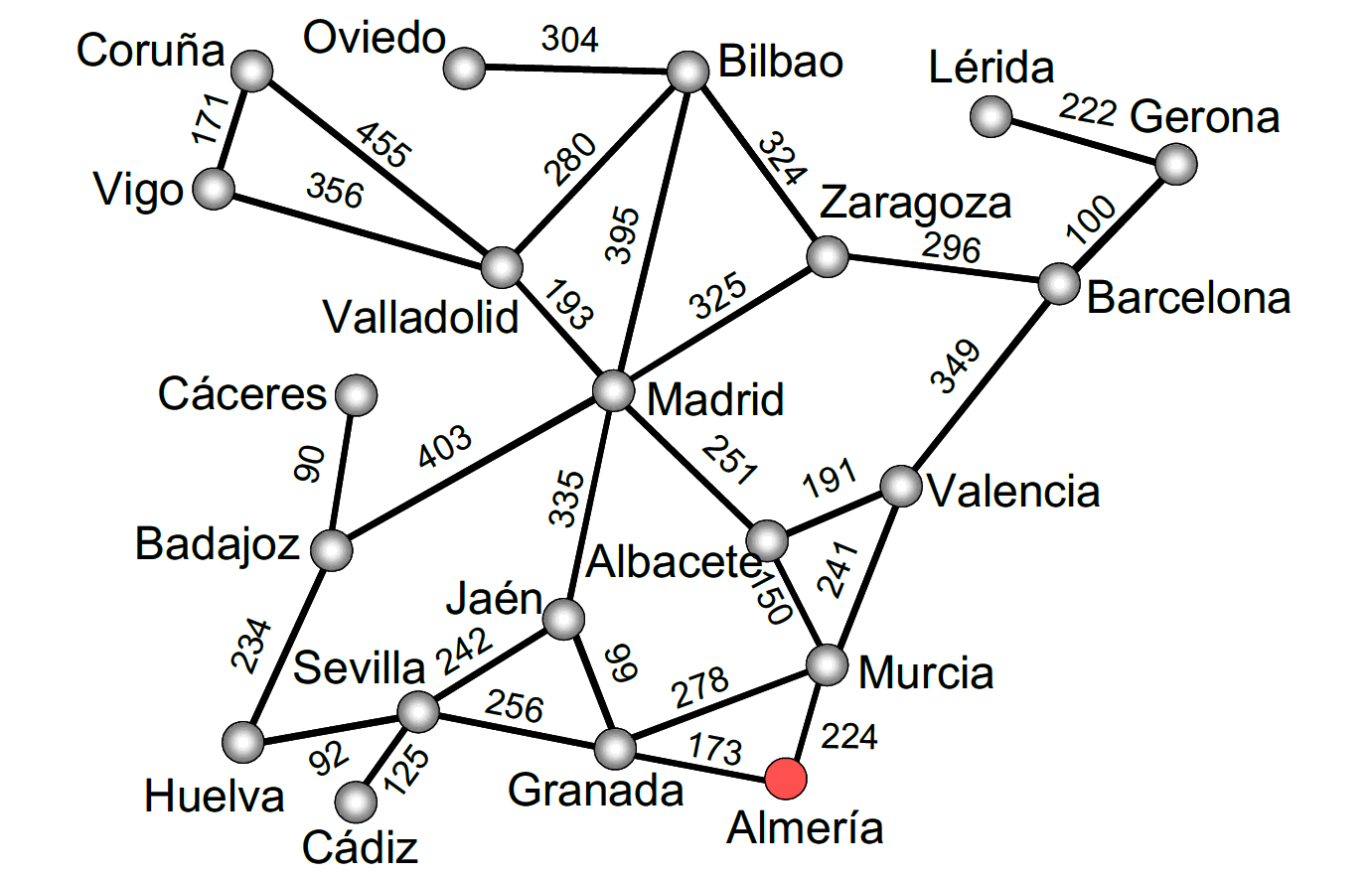
First of all, there is the reduced network of roads of EDAland (Figure 1) that connects the large population centers (cities) of the country (21 cities and 29 roads), together with the estimate in thousands of euros of what it would cost to pave the route between two cities (same road network as in EDA I). For example, paving the road that connects Almería with Granada would cost 173,000 euros. This network will be used to test our greedy algorithms and verify their correct operation.
Once you check the correct operation of our greedy algorithms in the reduced network of roads, we will execute them in the national network of roads of EDALand that the Ministry has (1053 population centers and 2017 roads with the estimated cost of paving them in thousands of euros) (Figure 2, adapted from roads graph published in [1]), and in this way we would already have the total budget that the global work would cost, which, as we already know, must be the least possible (main requirement of the Ministry).
Work to develop
You must propose and implement two solutions (algorithms) with the greedy scheme to the problem posed. An algorithm will choose the lowest cost edge to pave among those that are available, keeping the subnet being built connected. The other will select the edge with the lowest cost among all the remaining ones, even if the resulting subnetwork is not connected. For the first case, two variants of the algorithm will be implemented, using a priority queue and without.
In addition, you will need to implement a random network generator (unoriented, positively valued, connected graphs). In which, given a valid number of vertexes and a valid number of edges, it will generate a random network in a text file on disk (following the same format as real networks) so that it can then be loaded and run the greedy algorithms on much larger networks. .
0 // undirected
n // number of vertexes
1 // vertex 1
2 // vertex 2
...
n // vertex n
m // number of edges
1 2 25.0 // vi vj costij
// like this until completing m entries/edgesTo do this, you must complete the following sections:
-
Study of the implementation: Explain the most important details of the implementation, both of the data structures used to store the network, and of the implemented greedy algorithms. The code must be reasonably well documented (JavaDoc).
-
Theoretical study: Study the execution times of the implemented algorithms, depending on the number of population centers (vertexes) and the number of paths (edges). Also compare the proposed algorithms, taking into account the characteristics of the network (graph) and the chosen implementation techniques. Justifiably answer the following questions: (1) Is the result of the execution of each algorithm unique? (2) Should the result of the execution of the two algorithms be the same? Why? (3) If the weight of the edges were the distance between two cities, with the resulting structure, can we determine the minimum path between any two pairs of cities?
-
Experimental study: Validation of the greedy algorithms implemented on the real networks (EDAland) provided. To do this, the execution times of the implemented algorithms must be obtained and compared. The theoretical and experimental results will be contrasted, checking if the experimental ones confirm the previously analyzed theoretical ones. The experiments carried out will be justified, and in case of discrepancy between the theory and the experiments, an attempt should be made to find a reasoned explanation. In addition, random networks (non-oriented, positively valued and connected graphs) will be generated, setting a number of vertexes (for example 5000, 10000, 15000 and 20000) and varying the number of edges in such a way that the graph is always connected (* random net generator*). On these new networks, the implemented greedy algorithms will be retested in order to compare them with a greater number of vertexes and edges.
Datafiles
Datafiles are available on the GitHub repository of this activity, in dataset folder:
-
graphPrimKruskal.txt⇒ file with the graph example from class slides of Prim and Kruskal algorithms. -
graphEDAland.txt⇒ file with reduced path network of EDAland (Figure 1) -
graphEDAlandLarge.txt⇒ file with EDAland national road network (Figure 2) -
graphEDAlandLargeVertices.txt⇒ file with vertexes and their x,y coordinates for graphical representation (volunteer).
Submissions
A public GitHub repository (same repository for all EDA II practices) with all the documentation and source code required in the practice must be submitted on date:
-
In said repository, create a new folder called
practica_2, where you create two subfolders, one for the documentation,docs, and one for the source code,sources. -
Memory that explains everything you have done in practice. The memory must have the format indicated below. If desired, you can also make a presentation of the practice.
-
Source code of the application, developed in JAVA, which solves everything raised in practice. Remember that you will have to measure execution times of your solutions, so you must include the necessary commands for this in the source code.
-
Test games that you consider appropriate to make sure that everything works correctly.
The memory of practice to deliver must be brief, clear and well written. This should include the following sections:
-
A brief introduction with a theoretical study of the algorithmic method used in this practice (greedy).
-
A section for each of the proposed sections to be developed in this practice (implementation study, theoretical study and experimental study). We must emphasize that the sections must be included in the same order in which they have been presented.
-
An annex with the design of the implemented code will also be included, with class diagram and any other diagram you consider useful, but do not include code here. In this annex, a list of the source files and a brief description of the content of each one must be included as well.
-
It is important to always include the bibliographical sources used (web, books, articles, etc.) and refer to them in the document.
Assessment
Each section will be evaluated independently, although it is a necessary condition to pass the internship that the implemented programs work correctly.
-
The implementation together with the documentation of the code will be valued out of 40%
-
The study of the implementation will be valued out of 10%
-
The theoretical study will be valued out of 15%
-
The experimental study will be valued out of 35%
It will be penalized not deliver the theoretical introduction section or a bad presentation of the report.
The defense of the code and memory by the teacher may be required.
Deadline
Deadline: April 17th 2020
References
-
[1] Gines García Mateos. The Traveler’s Challenge. Available online on http://dis.um.es/~ginesgm/retoviajante.html [Date of consult: 2022/03/19]