Estructuras de datos y Algoritmos II (EDA II). 2º Grado en Ingeniería Informática. Universidad de Almería
Version curso.2022 - reducida
Objetivos
-
Construir soluciones a un problema utilizando los métodos algorítmicos backtracking (vuelta atrás) y branch-and-bound (ramificación y poda). Analizar y comparar los algoritmos implementados desde diferentes perspectivas.
-
Realizar el análisis de la eficiencia de las soluciones aportadas, y una comparativa tanto desde el punto de vista teórico como práctico.
Requerimientos
Para superar esta práctica se debe realizar lo siguiente:
-
Recordar (de EDA I) las estructuras de datos más apropiadas para la resolución de problemas.
-
Conocer cómo implementar los esquemas algorítmicos backtracking y branch-and-bound para responder a una necesidad concreta (en este caso, resolver el problema del viajante de comercio y de ciclos hamiltonianos).
-
Evaluar los algoritmos implementados siguiendo los métodos backtracking y branch-and-bound, relacionando ambos métodos algorítmicos.
Enunciado del problema
Como sabemos, en EDAland existen ciudadanos muy característicos, entre ellos, nos encontramos a ‘Braulio el repartidor’, un trabajador incansable y responsable de Almería que lleva toda una vida repartiendo los periódicos del Hoy-Almeria por todo el país. Todas las madrugadas, cuando la editorial del Hoy-Almeria cierra el diario y salen los primeros ejemplares de la imprenta, Braulio está ahí, con su furgoneta, listo para repartirlos entre todas las ciudades de EDAland. Además de por su eficacia repartiendo, Braulio también destaca por ser una persona que tiene muy en cuenta su economía, y siempre procura escoger el circuito que le suponga recorrer la distancia más corta posible o realizar el menor gasto de combustible (y más ahora, al elevado precio que está) posible. Para ser tan eficaz, el bueno de Braulio se planteó tres cuestiones importantes. La primera consistía en conocer todos los posibles circuitos, partiendo desde Almería, que recorren cada ciudad, donde debe dejar un lote de periódicos, exactamente una vez y regresando posteriormente a Almería. La segunda cuestión consistía en determinar un circuito que recorra cada ciudad exactamente una vez, partiendo y regresando a Almería, y habiendo recorrido en total la menor distancia posible. La tercera y última cuestión consistía en determinar un circuito que recorra cada ciudad exactamente una vez, saliendo y volviendo a Almería y cuyo gasto en combustible sea el mínimo posible.
Para poder dar respuesta a las cuestiones que se plantea Braulio disponemos de la nueva red reducida de carreteras de EDAland (Figura 1). En EDAland se llevó a cabo un nuevo plan general de carreteras y se añadieron algunas nuevas vías (en azul) a la red anterior (práctica 2). Como podemos observar, ésta conecta a las grandes ciudades del país (21 ciudades con 41 carreteras), junto con la distancia en kilómetros entre dos ciudades. Por ejemplo, la distancia que conecta Almería con Granada es de 173 kilómetros. Esta red nos servirá para verificar el correcto funcionamiento de los algoritmos backtracking y branch-and-bound desarrollados.

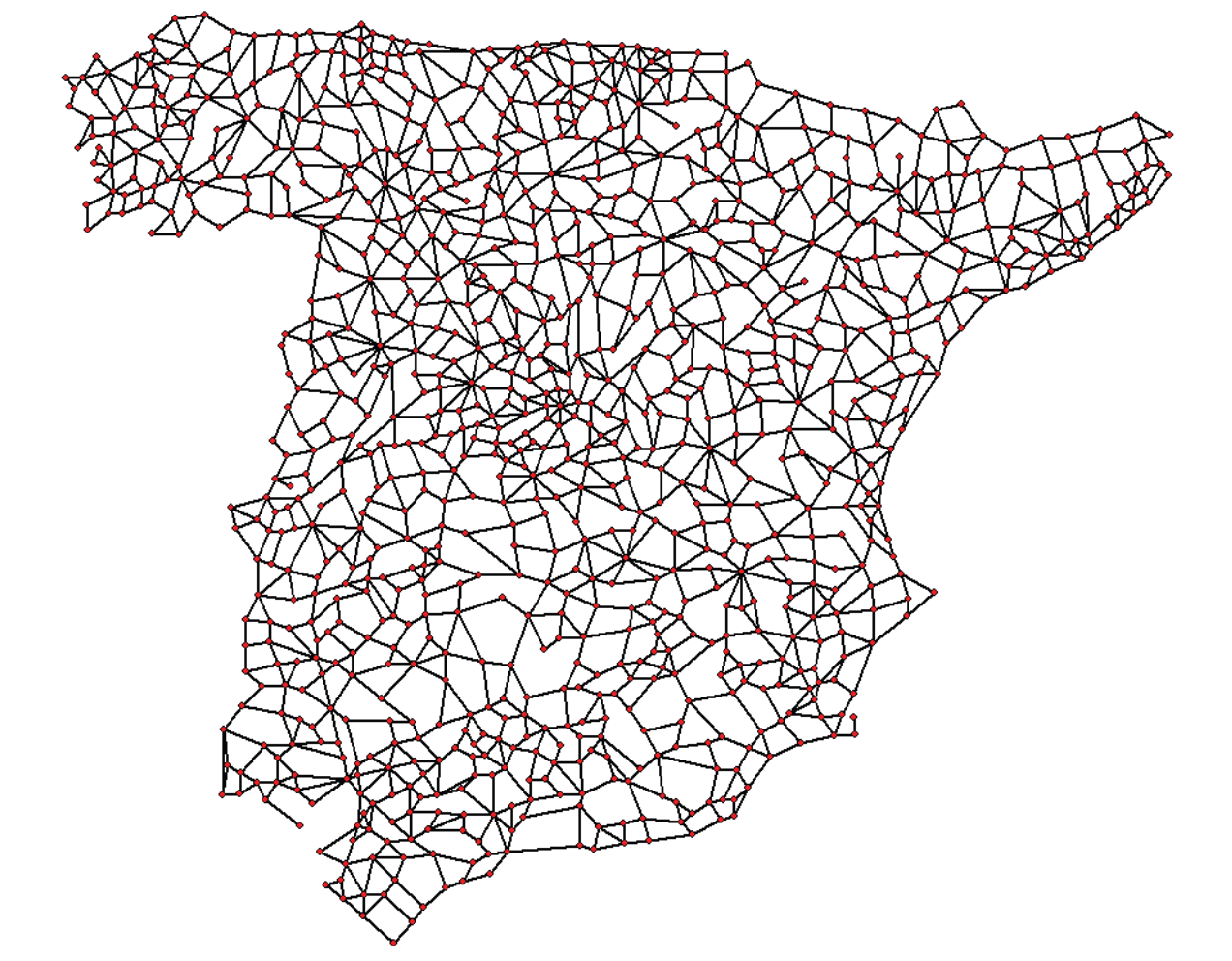
Una vez comprobado el correcto funcionamiento de nuestros algoritmos en la red reducida de caminos, analizaremos nuestros algoritmos en la red nacional de carreteras de EDALand (Figura 2, adaptado del grafo de ciudades y carreteras de [1]), que conecta a todos los núcleos de población del país (1053 núcleos de población con 2017 carreteras con la distancia que hay entre dos poblaciones). Ésta es la misma red de la práctica 2.
Trabajo a desarrollar
Deberá proponer e implementar soluciones con los esquemas algorítmicos de backtracking y branch-and-bound, según se requiera, a los problemas que se plantean a continuación.
-
(Backtracking) Determinar todos los posibles circuitos, si es que hubiera más de uno, partiendo desde Almería, que recorren cada ciudad de la nueva red reducida de carreteras de EDAland, donde Braulio debe dejar un lote de periódicos, exactamente una vez y regresar a Almería. Si hubiera más de uno, indique entre todos ellos el cirtuito de menor distancia.
Para este primer caso (Backtracking), implemente en Java el algoritmo El problema del viajante de las transparencias de clase de teoría, recomponiendolo para que funcione (ya que el de las transparecias puede tener algun error), definiendo las variables de forma que se adapten a la recursividad. Haga además un cálculo más o menos ajustado de las necesidades de pila que va a necesitar. En caso de tener problemas con el grafo de EDA I, utilice una matriz NxN.
-
(Branch-and-Bound) Determinar un circuito que, partiendo desde Almería, visite cada ciudad exactamente una vez, regresando a Almería y habiendo recorrido en total la menor distancia posible. Resolver este problema para la nueva red reducida de carreteras de EDAland.
-
(Opcional) Haciendo uso del algoritmo Branch-and-Bound implementado en los apartados anteriores, debe intentar obtener el circuito en la red nacional de carreteras completa, partiendo de un núcleo urbano cualquiera, que visite cada población exactamente una vez, regrese al núcleo de partida y tenga la menor distancia posible. Para comprobar que los algoritmos funcionan sobre dicha red, lleve a cabo una traza de la ejecución de los mismos en la que muestre su estado en función de la iteración o cada cierto tiempo. ¿Qué conclusiones obtiene del intento?. ¿Existe alguna forma de resolver el problema que se le ha planteado?. Indíquelo todo de forma razonada.
-
(Opcional) Lo mismo que el punto anterior, pero para el algoritmo Backtracking.
Para ello deberá realizar los siguientes apartados:
-
Estudio de la implementación: Explicar los detalles más importantes de la implementación llevada a cabo, tanto de las estructuras de datos utilizadas para resolver el problema en cuestión, como de los algoritmos implementados. El código debe de estar razonablemente bien documentado (
JavaDoc). -
Estudio experimental: Validación de los algoritmos de backtracking y branch-and-bound implementados sobre las redes de EDAland proporcionadas. Para ello, se deberán obtener y comparar los tiempos de ejecución de los algoritmos implementados.
Aproximación a la solución
Plantilla de implementación
A continuación tenéis un esquema o plantilla de la implementación del algoritmo branch-and-bound para el problema del TSP en un grafo representado por un mapa de adyacencia. Se trata de que completéis los bloques que faltan, marcados como comentarios dentro del código.
// return the minimum value of the edges
public double minimumEdgeValue() {
double minimum = Double.MAX_VALUE;
// Devuelve el menor valor de arista del grafo
// Dos bucles 'for' anidados
return minimum;
}
// TSP - BaB - Best-First
public ArrayList<Vertex> TSPBaB(Vertex source) {
TreeMap<Vertex, Double> neighborMap = adjacencyMap.get(source);
if (neighborMap == null)
return null;
minEdgeValue = minimumEdgeValue();
// Constructor de clase PathNode
PathNode firstNode = new PathNode(source);
PriorityQueue<PathNode> priorityQueue = new PriorityQueue<>();
priorityQueue.add(firstNode);
shortestCircuit = null;
double bestCost = Double.MAX_VALUE;
while(priorityQueue.size() > 0) {
// Y (PathNode) = menorElemento de la cola de prioridad en funcion de 'estimatedCost'
PathNode Y = priorityQueue.poll();
if (Y.getEstimatedCost() >= bestCost)
break;
else {
Vertex from = Y.lastVertexRes();
// Si el numero de vertices visitados es n
// y existe una arista que conecte 'from' con source
if ((Y.getVisitedVertices() == numberOfVertices()) &&
(containsEdge(from, source))) {
// Actualizar 'res' en Y añadiendo el vertice 'source'
// Actualizar 'totalCost' en Y con Y.totalCost + weight(from, source)
if (Y.getTotalCost() < bestCost) {
// Actualizar 'bestCost', 'shortestDistanceCircuit' y 'shortestCircuit'
}
}
else {
// Iterar para todos los vertices adyacentes a from,
// a cada vertice lo denominamos 'to'
if (vertice 'to' todavia no ha sido visitado en Y) { // hacer uso de la funcion 'isVertexVisited(vertex)' de PathNode
PathNode X = new PathNode(Y); // Uso de constructor copia
// Anadir 'to' a 'res' en X
// Incrementar en 1 los vertices visitados en X
// Actualizar 'totalCost' en X con Y.totalCost + weight(from, to)
// Actualizar 'estimatedCost' en X con X.totalCost + ((nVertices - X.getVisitedVertices() + 1) * minEdgeValue)
if (X.getEstimatedCost() < bestCost) {
priorityQueue.add(X);
}
}
}
}
}
}
return shortestCircuit;
}Otras clases necesarias
Además, necesitaréis la clase PathNode.java
protected class PathNode implements Comparable<PathNode> {
private ArrayList<Vertex> res; // result
private int visitedVertices; // The number of the visited vertices
private double totalCost; // The total cost of the path taken so far
private double estimatedCost; // Representing the lower bound of this state. * Priority
PathNode(Vertex vertexToVisit) {
res = new ArrayList<Vertex>();
res.add(vertexToVisit);
visitedVertices = 1;
totalCost = 0.0;
estimatedCost = numberOfVertices() * minEdgeValue;
}
PathNode(PathNode parentPathNode) {
// Constructor copia
}
@Override
public int compareTo(PathNode p) {
// El criterio de comparacion es 'estimatedCost' que se correponde con la prioridad
}
public ArrayList<Vertex> getRes() {
return res;
}
public void addVertexRes(Vertex v) {
this.res.add(v);
}
public Vertex lastVertexRes() {
// Devuelve el ultimo vertice que se ha anadido al camino (ultimo elemento de 'res')
}
public boolean isVertexVisited(Vertex v) {
// Se ha visitado el vertice v si esta actualmente en 'res'. Una sola linea
}
public int getVisitedVertices() {
return visitedVertices;
}
public void setVisitedVertices(int visitedVertices) {
this.visitedVertices = visitedVertices;
}
public double getTotalCost() {
return totalCost;
}
public void setTotalCost(double totalCost) {
this.totalCost = totalCost;
}
public double getEstimatedCost() {
return estimatedCost;
}
public void setEstimatedCost(double estimatedCost) {
this.estimatedCost = estimatedCost;
}
}Método main con argumentos
Para la ejecución de los algoritmos, y con el objetivo de facilitar la ejecución de los distintos algoritmos implementados sobre los distintos archivos de datos sin tener que modificar el código fuente, se muestra cómo diseñar el método principal (main) para que permita recibir argumentos, separados por espacios en blanco. Para ello, se usará el parámetro args en la llamada a main, como en el siguiente ejemplo:
package org.ualeda2.mainWithArguments;
public class MainWithArguments {
public static void main(String[] args) {
// TODO Auto-generated method stub
System.out.println("The number of arguments is: "+args.length);
System.out.println("Your first argument is: "+args[0]);
System.out.println("Your second argument is: "+args[1]);
}
}Entregas
Se ha de entregar, en fecha, en el repositorio privado de GitHub para todas las prácticas de la asignatura con acceso para el/los profesor/es que evalúa/n las prácticas (mismo repositorio para todas las prácticas de EDA II), con la documentación y el código fuente requerido en la práctica:
-
En dicho repositorio debe estar la carpeta llamada
practica_4, donde debe haber como mínimo una carpetasrcpara el código fuente, y una carpetadocspara la documentación, incluyendo los JavaDoc y los diagramas de clase generados automáticamente a partir del código fuente, siguiendo la estructura de proyecto Java descrita en la práctica anterior. -
Memoria simplificada que explique lo que habéis realizado en la práctica. La memoria deberá tener el formato que se indica a continuación.
-
Código fuente de la aplicación, desarrollada en JAVA, que resuelva todo lo planteado en la práctica. Recordad que tendréis que medir tiempos de ejecución de vuestras soluciones por lo que deberéis incluir las órdenes necesarias para ello en el código fuente. Igualmente, si ejecuta sus algoritmos sobre la red grande de EDAland, no olvidéis mostrar la traza de la ejecución de los mismos en la que muestre su estado en función de la iteración o cada cierto tiempo.
La memoria de práctica a entregar debe ser breve, clara y estar bien escrita. Ésta debe incluir las siguientes secciones:
-
Una sección para cada uno de apartados propuestos a desarrollar en esta práctica (estudio de la implementación y estudio experimental).
-
Se incluirá también un anexo con el diseño del código implementado con diagramas de clases (copiar aquí los diagramas de clases generados automáticamente).
Evaluación
Cada apartado se evaluará independientemente, aunque es condición necesaria para aprobar la práctica que los programas implementados funcionen correctamente.
-
La implementación junto con la documentación del código se valorará sobre un 60%
-
El estudio de la implementación se valorará sobre un 20%
-
El estudio experimental se valorará sobre un 20%
Se podrá requerir la defensa del código y de la memoria por parte de profesor.
Fecha de entrega
Fecha de entrega: 5 de Junio
Resultados (Nuevo)
La ejecución de los algoritmos en la nueva red reducida de carreteras de EDAland (Figura 1) debe dar como resultado un total de 34 circuitos. A continuación se muestra un ejemplo de resultados de ejecución (se muestran solo 3 de los 34 circuitos). El más corto de todos debe destacarse también al final:
Almeria - Granada - Cadiz - Huelva - Sevilla - Jaen - Badajoz - Caceres - Madrid - Valladolid - Vigo - Corunya - Oviedo - Bilbao - Lerida - Gerona - Barcelona - Zaragoza - Valencia - Albacete - Murcia - Almeria ==> 4999.0
Almeria - Granada - Cadiz - Huelva - Sevilla - Jaen - Badajoz - Caceres - Valladolid - Vigo - Corunya - Oviedo - Bilbao - Lerida - Gerona - Barcelona - Valencia - Zaragoza - Madrid - Albacete - Murcia - Almeria ==> 5271.0
Almeria - Granada - Cadiz - Huelva - Sevilla - Jaen - Badajoz - Caceres - Valladolid - Vigo - Corunya - Oviedo - Bilbao - Lerida - Gerona - Barcelona - Zaragoza - Madrid - Albacete - Valencia - Murcia - Almeria ==> 5192.0
...
...
Number of circuits: 34
Shortest circuit:
Almeria - .... ==> ...Referencias
-
[1] Gines García Mateos. El Reto del Viajante. Disponible online en http://dis.um.es/~ginesgm/retoviajante.html [Fecha de consulta: 19/03/2022]